Brahmagupta
(→Quadratic Indeterminate Equations: The Cakravāla Method) |
(→Quadratic Indeterminate Equations: The Cakravāla Method) |
||
| (One intermediate revision by one user not shown) | |||
| Line 324: | Line 324: | ||
√2 ≈ 1+ 1/3 + 1/3.4 - 1/3.4.34 = 577/408 [(577)<sup>2</sup> - 2 (408)<sup>2</sup> = 1] | √2 ≈ 1+ 1/3 + 1/3.4 - 1/3.4.34 = 577/408 [(577)<sup>2</sup> - 2 (408)<sup>2</sup> = 1] | ||
| − | मलू ं ि ध े वगाद ् गणु कगणु ािद यतु िवहीना । आ वधो गणु कगणु ः सहा यघातने कृ तम यम॥् व वध ै यं थमं पे ः पे वधत ु यः। | + | |
| − | + | ||
| + | मलू ं ि ध े वगाद ् गणु कगणु ािद यतु िवहीना । | ||
| + | |||
| + | आ वधो गणु कगणु ः सहा यघातने कृ तम यम॥् | ||
| + | |||
| + | व वध ै यं थमं पे ः पे वधत ु यः। | ||
| + | |||
| + | पे श ो ध क त े म लू े पे क े प ॥े | ||
Latest revision as of 10:20, 11 January 2018
This is a collection of articles archived for the excellence of their content. |
Contents |
[edit] Who was Brahmagupta?
J.P.Bohre, NCERT- Contribution of Indian Mathematicians
(1) Brahmagupta was born in 598 A.D.in Bhinmal city in the state of Rajasthan. He was a mathematician and astronomer, who wrote many important works on mathematics and astronomy. His best known work is the “Brahmasphuta‐siddhanta”, written in 628 AD in Bhinmal.
(2) He was the first to use zero as a number. He gave rules to compute with zero.
(3) He gave four methods of multiplication.
(4) He gave following formulae, used in G.P. series
a+ar+ar2+ar3 +..........+arn‐1 =a(rn ‐1)/( r‐1)
(5) He gave the following formulae(Brahmagupta’s formula):
Area of a cyclic quadrilateral with side a,b,c,d = √(s‐a)(s‐b)(s‐c)(s‐d), where 2s= a+b+c+d.
Length of its diagonals= {√bc+ad/ √(ab+cd)} (ac+bd), {√ab+cd/ √(bc+ad)} (ac+bd).
[edit] Biography
MacTutor- School of Mathematics and Statistics, University of St Andrews, Scotland
URL: Stable URL
Article by: J J O'Connor and E F Robertson
Born: 598 in (possibly) Ujjain, India
Died: 670 in India
Brahmagupta, whose father was Jisnugupta, wrote important works on mathematics and astronomy. In particular he wrote Brahmasphutasiddhanta, in 628. The work was written in 25 chapters and Brahmagupta tells us in the text that he wrote it at Bhillamala which today is the city of Bhinmal. This was the capital of the lands ruled by the Gurjara dynasty.
Brahmagupta became the head of the astronomical observatory at Ujjain which was the foremost mathematical centre of ancient India at this time. Outstanding mathematicians such as Varahamihira had worked there and built up a strong school of mathematical astronomy.
In addition to the Brahmasphutasiddhanta Brahmagupta wrote a second work on mathematics and astronomy which is the Khandakhadyaka written in 665 when he was 67 years old. We look below at some of the remarkable ideas which Brahmagupta's two treatises contain. First let us give an overview of their contents.
The Brahmasphutasiddhanta contains twenty-five chapters but the first ten of these chapters seem to form what many historians believe was a first version of Brahmagupta's work and some manuscripts exist which contain only these chapters. These ten chapters are arranged in topics which are typical of Indian mathematical astronomy texts of the period. The topics covered are: mean longitudes of the planets; true longitudes of the planets; the three problems of diurnal rotation; lunar eclipses; solar eclipses; risings and settings; the moon's crescent; the moon's shadow; conjunctions of the planets with each other; and conjunctions of the planets with the fixed stars.
The remaining fifteen chapters seem to form a second work which is major addendum to the original treatise. The chapters are: examination of previous treatises on astronomy; on mathematics; additions to chapter 1; additions to chapter 2; additions to chapter 3; additions to chapter 4 and 5; additions to chapter 7; on algebra; on the gnomon; on meters; on the sphere; on instruments; summary of contents; versified tables.
Brahmagupta's understanding of the number systems went far beyond that of others of the period. In the Brahmasphutasiddhanta he defined zero as the result of subtracting a number from itself. He gave some properties as follows:-
When zero is added to a number or subtracted from a number, the number remains unchanged; and a number multiplied by zero becomes zero.
He also gives arithmetical rules in terms of fortunes (positive numbers) and debts (negative numbers):-
A debt minus zero is a debt.
A fortune minus zero is a fortune.
Zero minus zero is a zero.
A debt subtracted from zero is a fortune.
A fortune subtracted from zero is a debt.
The product of zero multiplied by a debt or fortune is zero.
The product of zero multipliedby zero is zero.
The product or quotient of two fortunes is one fortune.
The product or quotient of two debts is one fortune.
The product or quotient of a debt and a fortune is a debt.
The product or quotient of a fortune and a debt is a debt.
Brahmagupta then tried to extend arithmetic to include division by zero:-
Positive or negative numbers when divided by zero is a fraction the zero as denominator.
Zero divided by negative or positive numbers is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator.
Zero divided by zero is zero.
Really Brahmagupta is saying very little when he suggests that n divided by zero is n/0. He is certainly wrong when he then claims that zero divided by zero is zero. However it is a brilliant attempt to extend arithmetic to negative numbers and zero.
We can also describe his methods of multiplication which use the place-value system to its full advantage in almost the same way as it is used today. We give three examples of the methods he presents in the Brahmasphutasiddhanta and in doing so we follow Ifrah in [4]. The first method we describe is called "gomutrika" by Brahmagupta. Ifrah translates "gomutrika" to "like the trajectory of a cow's urine". Consider the product of 235 multiplied by 264. We begin by setting out the sum as follows:
2 235
6 235
4 235
---
Now multiply the 235 of the top row by the 2 in the top position of the left hand column. Begin by 2 × 5 = 10, putting 0 below the 5 of the top row, carrying 1 in the usual way to get
2 235
6 235
4 235
---
470
Now multiply the 235 of the second row by the 6 in the left hand column writing the number in the line below the 470 but moved one place to the right
2 235
6 235
4 235
---
470
1410
Now multiply the 235 of the third row by the 4 in the left hand column writing the number in the line below the 1410 but moved one place to the right
2 235
6 235
4 235
---
470
1410
940
Now add the three numbers below the line
2 235
6 235
4 235
---
470
1410
940
---
62040
The variants are first writing the second number on the right but with the order of the digits reversed as follows
235 4
235 6
235 2
---
940
1410
470
---
62040
The third variant just writes each number once but otherwise follows the second method
235
---
940 4
1410 6
470 2
---
62040
Another arithmetical result presented by Brahmagupta is his algorithm for computing square roots. This algorithm is discussed in [15] where it is shown to be equivalent to the Newton-Raphson iterative formula. Brahmagupta developed some algebraic notation and presents methods to solve quardatic equations. He presents methods to solve indeterminate equations of the form ax + c = by. Majumdar in [17] writes:-
Brahmagupta perhaps used the method of continued fractions to find the integral solution of an indeterminate equation of the type ax + c = by.
In [17] Majumdar gives the original Sanskrit verses from Brahmagupta's Brahmasphuta siddhanta and their English translation with modern interpretation.
Brahmagupta also solves quadratic indeterminate equations of the type ax2 + c = y2 and ax2 - c = y2. For example he solves 8x2 + 1 = y2 obtaining the solutions (x, y) = (1, 3), (6, 17), (35, 99), (204, 577), (1189, 3363), ... For the equation 11x2 + 1 = y2 Brahmagupta obtained the solutions (x, y) = (3, 10), (161/5, 534/5), ... He also solves 61x2 + 1 = y2 which is particularly elegant having x = 226153980, y = 1766319049 as its smallest solution.
A example of the type of problems Brahmagupta poses and solves in the Brahmasphutasiddhanta is the following:-
Five hundred drammas were loaned at an unknown rate of interest, The interest on the money for four months was loaned to another at the same rate of interest and amounted in ten mounths to 78 drammas. Give the rate of interest.
Rules for summing series are also given. Brahmagupta gives the sum of the squares of the first n natural numbers as n(n+1)(2n+1)/6 and the sum of the cubes of the first n natural numbers as (n(n+1)/2)2. No proofs are given so we do not know how Brahmagupta discovered these formulae.
In the Brahmasphutasiddhanta Brahmagupta gave remarkable formulae for the area of a cyclic quadrilateral and for the lengths of the diagonals in terms of the sides. The only debatable point here is that Brahmagupta does not state that the formulae are only true for cyclic quadrilaterals so some historians claim it to be an error while others claim that he clearly meant the rules to apply only to cyclic quadrilaterals.
Much material in the Brahmasphutasiddhanta deals with solar and lunar eclipses, planetary conjunctions and positions of the planets. Brahmagupta believed in a static Earth and he gave the length of the year as 365 days 6 hours 5 minutes 19 seconds in the first work, changing the value to 365 days 6 hours 12 minutes 36 seconds in the second book the Khandakhadyaka. This second values is not, of course, an improvement on the first since the true length of the years if less than 365 days 6 hours. One has to wonder whether Brahmagupta's second value for the length of the year is taken from Aryabhata I since the two agree to within 6 seconds, yet are about 24 minutes out.
The Khandakhadyaka is in eight chapters again covering topics such as: the longitudes of the planets; the three problems of diurnal rotation; lunar eclipses; solar eclipses; risings and settings; the moon's crescent; and conjunctions of the planets. It contains an appendix which is some versions has only one chapter, in other versions has three.
Of particular interest to mathematics in this second work by Brahmagupta is the interpolation formula he uses to compute values of sines. This is studied in detail in [13] where it is shown to be a particular case up to second order of the more general Newton-Stirling interpolation formula.
[edit] Brahmagupta II’s work
[edit] Brahmagupta's Formula
Jim Wilson, The University of Georgia
Problem: Develop a proof for Brahmagupta's Formula.
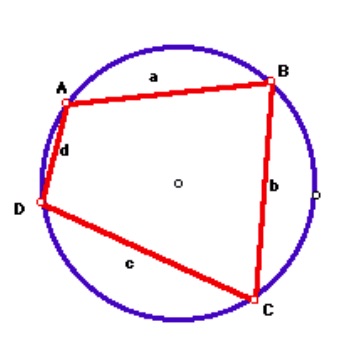
From: Jim Wilson, The University of Georgia
Who was Brahmagupta?
Brahmagupta's formula provides the area A of a cyclic quadrilateral (i.e., a simple quadrilateral that is inscribed in a circle) with sides of length a, b, c, and d as
√(s-a)(s-b)(s-c)(s-d)
where s is the semiperimeter
s= a+b+c+d/2
If ABCD is a rectangle the formula is clear.
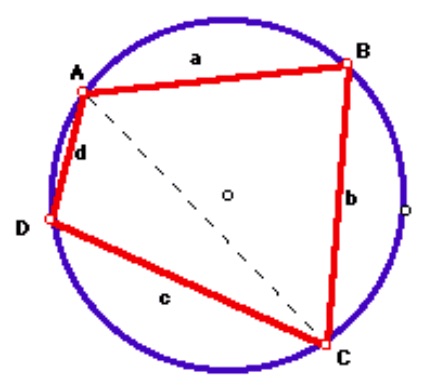
From: Jim Wilson, The University of Georgia
Consider the chord AC.
The angle that subtends a chord has measure that is half the measure of the intercepted arc. But the chord AC is simultaneously subtended by the angle at B and by the angle at D. There for the sum of these angles is 180 degrees. Opposite angles of a cyclic quadrilateral are supplemental.
Assume the quadrilateral is not a rectangle. WNLOG, extend AB and CD until they meet at P.
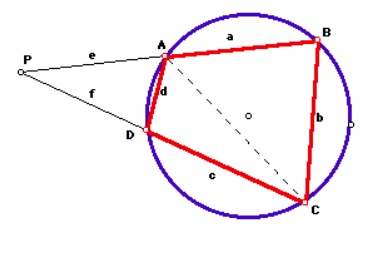
From: Jim Wilson, The University of Georgia
Label the extensions outside the circle e and f.
Now, triangles PBC and PDA are similar. Further, the ratio of similarity is d/b. Therefore the ratio of similarity of their areas is the square of this ratio, or,
Area of triangle PDA= d2/b2 (Area of triangle PBC)
Now the area of the quadrilateral ABCD is the area of the larger triangle PBC less the area of the smaller triangle PDA. If A is the area of the quadrilateral and T is the area of triangle PBC
A= T-(d2 / b2) T = 1-(d2/b2) T = (b2-d2/b2)T
OR
A= {(b2-d2) / b2 } T
Now,
1. Heron's formula can be used to express the area of triangle PBC
2. The similarity of triangles PBC and PAD can be use to effect various (but tedious) substitutions.
With appropriate perseverance and and algebraic subsitiutions/simplifications, Brahmagupta's theorem can be derived.
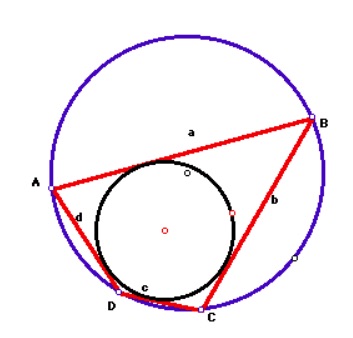
From: Jim Wilson, The University of Georgia
Extensions:
1. If ABCD is a quadrilateral with sides of length a, b, c, and d, such that ABCD is both cyclic and has a circle inscribed in it, then use Brahmagupta's formula to show that the area of the quadrilateral is
A= √abcd
2. Consider Brahmagupta's formula as one side, say the one of length d wnlog, varies and approaches zero in length.
3. Use Brahmagupta's formula to develop equations for the length of the two diagonals of the quadrilateral.
[edit] Quadratic Indeterminate Equations: The Cakravāla Method
M.D.Srinivas, CENTRE FOR POLICY STUDIES
OUTLINE
• The vargaprakçti equation X2 – D Y2 = K, and Brahmagupta’s bhāvanā process (c. 628 CE).
• The cakravāla method of solution of Jayadeva (c. 10th cent) and Bhāskara (c.1150).
• Bhāskara’s examples X2 – 61Y2 = 1, X2 – 67Y2 = 1.
• Analysis of the cakravāla method by Krishnaswami Ayyangar.
• History of the so called "Pell’s Equation" X2 - D Y2 = 1.
• Solution of "Pell’s equation" by expansion of √D into a simple continued fraction (c. 18th cent).
• Bhāskara semi-regular continued fraction expansion of √D
• Optimality of the cakravāla method.
In Chapter XVIII of his Brāhmasphuña-siddhānta (c.628 CE), Brahmagupta considers the problem of solving for integral values of X, Y, the equation
X2 – D Y2 = K,
given a non-square integer D > 0, and an integer K.
X is called the larger root (jyeùñha-mūla), Y is called the smaller root (kaniùñha-mūla), D is the prakçti, K is the kùepa.
One motivation for this problem is that of finding rational approximations to square-root of D. If X, Y are integers such that X2 - D Y2 = 1, then,
|√D-(x/y) | ≤1/2xy,
The Śulva-sūtra approximation (prior to 800 BCE):
√2 ≈ 1+ 1/3 + 1/3.4 - 1/3.4.34 = 577/408 [(577)2 - 2 (408)2 = 1]
मलू ं ि ध े वगाद ् गणु कगणु ािद यतु िवहीना ।
आ वधो गणु कगणु ः सहा यघातने कृ तम यम॥्
व वध ै यं थमं पे ः पे वधत ु यः।
पे श ो ध क त े म लू े पे क े प ॥े